The Babylonian number system is old. four hundred clay tablets containing lists of Evelyn Lamb is a freelance math and science writer based in Salt Lake City, Utah. Hence it is commonplace to use their decimal counterparts, separated by commas, so that the number represented, for example, in cuneiform as: In such a system, the radix point is represented by a semicolon. In Mesopotamia the scribes of Babylon and the other big cities were impressing on clay tablets economic and administrative records, literary, religious and scientific works, word-lists, and mathematical problems and tables. The Open University is incorporated by Royal Charter (RC 000391), an exempt charity in England & Wales and a charity registered in Scotland (SC 038302). At least some of the examples we have appear to indicate problem-solving for its own sake rather than in order to resolve a concrete practical problem. Please be aware that due to the passage of time, the information provided on this page may be out of date or otherwise inaccurate, The fact that they had no symbol to indicate the zero digit means that this was not a true positional numeral system as such. They usually fit comfortably into the palm of a hand and are about an inch thick, although some are as small a postage stamp and others the size of a large book. xb```e``Yxb@i >_'@W0@./CbQ%\2%LtazNSz4[1?b t?M"\!| e
they tended to arrange the symbols into neat piles. But Babylonian reciprocal tables, which made calculations quicker, listed any two numbers that multiplied to a power of 60 as reciprocals. For example, 5 and 12 are reciprocals in this sense because they multiply to 60. (2020, August 27). As a result of the extensive excavations of the nineteenth century there are many more tablets available in museums and universities throughout the world than have yet been translated or even catalogued. Starting as early as the 4th millennium BCE, they began using a small clay cone to represent one, a clay ball for ten, and a large cone for sixty. is shown at the right. 58 23
were too many symbols, so they turned the stylus on its side to make a different
<]>>
The Sumerians developed the earliest known writing system a pictographic writing system known as cuneiform script, using wedge-shaped characters inscribed on baked clay tablets and this has meant that we actually have more knowledge of ancient Sumerian and Babylonian mathematics than of early Egyptian mathematics. N.S.

The teacher of In much later sources, mainly astronomical texts dating from 300 BCE onwards, a special symbol is introduced to mark empty places within numerals; but not at the end of a numeral, so the absolute value of the whole is still left floating. It started about 1900 BC to 1800 BC but
It is quite a complicated system, but it was used by other
The Open University is authorised and regulated by the Financial Conduct Authority in relation to its secondary activity of credit broking. They never made the leap to using a zero symbol at the end of a number to eliminate the ambiguity completely. Believe it or not, this didn't worry them. X X t 2 2 2 2 2 2 2 F F _ 2 $ R ^ 2 a a a 2 2 a ^ 2 2 a % V @ 2 2 N / 0 _ You could say that there should be a bigger gap for 3601, since the gap represents nothing in the sixty column, but how easy to make a mistake! Both these have two symbols for one. Information on For informal everyday arithmetic, they used a decimal system which was the decimal part of the full sexagesimal system. She has been featured by NPR and National Geographic for her ancient history expertise. The Babylonians also developed another revolutionary mathematical concept, something else that the Egyptians, Greeks and Romans did not have, a circle character for zero, although its symbol was really still more of a placeholder than a number in its own right. Thanks for reading Scientific American. cuneiform prepared an example on the left half of a soft > 2 4 1 5@ t bjbj22 . The Babylonian number system uses base 60 (sexagesimal) instead of 10. The number system as used in the Old Babylonian empire was a positional numeral system where the number base was a combination of decimal (base $10$) and sexagesimal (base $60$). 0000001159 00000 n
Scientific American is part of Springer Nature, which owns or has commercial relations with thousands of scientific publications (many of them can be found at, In Praise of Proofs by Contradiction that Aren't, Mathematics, Live: A Conversation with Evelyn Boyd Granville, public domain, via sugarfish and Wikimedia Commons, Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322, One Weird Trick to Make Calculus More Beautiful, When Rational Points Are Few and Far Between. Like the Egyptians, the Babylonians used two
They wrote their numerals from left to right using just two symbols: If there was no value in a place (which is what our zero symbol signifies) a space was sometimes left but otherwise meant 1, 60, or 3600 (or indeed 1/60, 1/3600 etc) according to context. Babylonian Clay tablets from c. 2100 BCE showing a problem concerning the area of an irregular shape. you line the numbers up so their units are in the same column. Indeed, we even have what appear to school exercises in arithmetic and geometric problems. The Babylonian approach to solving them usually revolved around a kind of geometric game of slicing up and rearranging shapes, although the use of algebra and quadratic equations also appears. Nearly all of the texts that give us our fullest understanding of Babylonian mathematics date from the Old Babylonian Period about 1800-1600 BCE. 25 means two tens, five ones." oldest surviving document on number theory. excavated since the first half of the nineteenth century. Average rating 0 out of 5, based on 0 rating. (subscript D) numbers 12, 37, 97, 65 and Because when youre writing in base 60 without a zero, 60 looks just like 1! For more detail, see our Archive and Deletion Policy. I am using a yellow background to represent the clay! So the left-hand column were units, the second, multiples of 60, the third, multiplies of 3,600, and so on. 0000000756 00000 n
The base 5 system likely originated from ancient peoples using the digits on one hand to count. Retrieved from https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679. If we interpret 12 as 12/60 (1/5), then we can multiply it by 5 to make 1. Unlike those of the Egyptians, Greeks and Romans, Babylonian numbers used a true place-value system, where digits written in the left column represented larger values, much as in the modern decimal system, although of course using base 60 not base 10.
Most of the tablets are rectangular but there are some that are round in shape. "Babylonian Mathematics and the Base 60 System." x2) naturally arose in the context of the meaurement of land, and Babylonian mathematical tablets give us the first ever evidence of the solution of quadratic equations.

Enter number:
(There is no connection between angle minutes & seconds and time minutes & seconds. One of the strange consequences of the lack of zero comes up in reciprocals. The number $25 \, 267$ is represented in the Babylonian number system as: The number represented in the Babylonian number system as: https://proofwiki.org/w/index.php?title=Definition:Babylonian_Number_System&oldid=478537, $\mathsf{Pr} \infty \mathsf{fWiki}$ $\LaTeX$ commands, Creative Commons Attribution-ShareAlike License, This page was last modified on 17 July 2020, at 06:32 and is 0 bytes. Babylon was just one city in ancient Mesopotamia, but the usage is fairly standard. The solution is then generally given through a series of instructions. The symbol for sixty seems to be exactly
followed by examples of the decimal As in Egypt, Sumerian mathematics initially developed largely as a response to bureaucratic needs when their civilization settled and developed agriculture (possibly as early as the 6th millennium BCE) for the measurement of plots of land, the taxation of individuals, etc. Sixty is a very good number for a base. The Babylonians didnt have a symbol for zero. It is a base 10 / base 60 system, and quite hard to understand. Babylonian Mathematics and the Base 60 System. The biggest difficulty my students and I had deciphering these numbers was not the fact that there were so many extra numerals to keep track of. 0000002305 00000 n
ThoughtCo, Aug. 27, 2020, thoughtco.com/why-we-still-use-babylonian-mathematics-116679. hour are cultural artifacts passed down to It was made in Babylon between 1900 and 1600 As I told my class on Thursday, the theme of the first week of our math history course was easy algebra is hard in base 60. We started the semester in ancient Mesopotamia, trying to understand Babylonian* mathematical notation and decipher Plimpton 322, an enigmatic tablet from about 1800 BCE. over their own systems. The content of these pages has not been reviewed or The Babylonians even knew the formula thats today known as the Pythagorean theorem. Gill, N.S. B.C. were working their way towards a positional system (see below). strange happened at sixty (see below). You many wonder why they seemed to like the number sixty so much. Why would this definition of reciprocal make sense? The system surfaced circa 3100 BCE, according to The New York Times. For fractional numbers there was no actual radix point. We have evidence of the development of a complex system of metrology in Sumer from about 3000 BCE, and multiplication and reciprocal (division) tables, tables of squares, square roots and cube roots, geometrical exercises and division problems from around 2600 BCE onwards. tables of more than half a million engraved in their written cuneiform script which have been Explore our digital archive back to 1845, including articles by more than 150 Nobel Prize winners. Discover world-changing science. However, the number 60 was represented by the same symbol as the number 1 and, because they lacked an equivalent of the decimal point, the actual place value of a symbol often had to be inferred from the context. 12 months, 12 inches, 12 pence, 2 x 12 hours, etc). 23 would be shown as ). Sachs. 0000002679 00000 n
Today, with the most advanced technology ever, societies still must make temporal adjustments almost 25 times per century to the calendar and a few seconds every few years to the atomic clock. clay tablet and the student was instructed to copy that The Babylonian mathematics system may not be as popular as it once was, but it has advantages over the base 10 system because the number 60 has more divisors than any smaller positive integer, the Times pointed out. In addition, the Sumerians and Babylonians needed to describe quite large numbers as they attempted to chart the course of the night sky and develop their sophisticated lunar calendar. When the two groups traded together, they evolved a system based on 60 so both could understand it.. 0
The base isn't what makes calculations in base 60 difficult, it's the fact that mathematical culture of the people who made it is so different from ours. https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679 (accessed July 21, 2022). Almost invariably the central purpose of a Babylonian problem is the computation of a specific number. ones to represent two, three ones for three, and so on, up to nine. If you want to add large numbers (and you've lost your calculator!) The Babylonians used geometric shapes in their buildings and design and in dice for the leisure games which were so popular in their society, such as the ancient game of backgammon. The writing is in cuneiform (wedge-shaped) script and it is usually found on the front and the back of the tablets, and sometimes on the side as well. For their numeral system, the Babylonians used the sexagesimal (base 60) place-value system. interactive media may no longer work. us from the Babylonians. like one and one, and so on. ThoughtCo. sexagecimal, number system which is cultures, such as the Greeks, as it had advantages
Over the course of the third millennium, these objects were replaced by cuneiform equivalents so that numbers could be written with the same stylus that was being used for the words in the text. Eleven was ten and one, twelve was ten and one and one, twenty was ten
0000011151 00000 n
It is for similar reasons that 12 (which has factors of 1, 2, 3, 4 and 6) has been such a popular multiple historically (e.g. index. The oldest documented zero is surprisingly modern: its in a temple in India, and it dates from about 875 CE. the page authors. We spent some time in class calculating Babylonian reciprocals, (pdf) and it was surprisingly difficult. Designated PLIMPTON 322 in the Plimpton Collection at Columbia University, it is the Unlike the Hindu-Arabic numerals we use today, Babylonian numerals look like the numbers they represent. Those numbers also multiply together to make 1. Create your free account or Sign in to continue. 0000002755 00000 n
preserved in tablets made by pressing into There are tables of squares, multiplication tables, tables of reciprocals (used for division), tables of square and cube roots, combined tables where several of these are present, tables for working out compound interest, tables of weights and measures, and others. Others list the squares of numbers up to 59, the cubes of numbers up to 32 as well as tables of compound interest. example on the right half. A F F 2 2 2 2 A 2 \ h J h. With only their table of squares (albeit going up to a monstrous 59 squared), they could compute the product of two integers, a and b, using a formula similar to: ab = [(a + b)2 - (a - b)2]/4. trailer
Cuneiform In Plimpton 322, the tablet we studied in class, there are some gaps between numerals that represent zeros in the middle of a number, the way the 0 in 101 represents zero tens. Log into OpenLearn to leave reviews and join in the conversation. Typical examples involve the flooding of a field to a depth of one finger for irrigation, and finding the length of a broken reed used for measuring a field! Their geometry extended to the calculation of the areas of rectangles, triangles and trapezoids, as well as the volumes of simple shapes such as bricks and cylinders (although not pyramids). ), Jo Edkins 2006 - Return to Numbers
Sixty one is sixty and one, which therefore looks
(subscript S) equivalents. below. You can also do arithmetic far easier, although I'm not quite sure about learning multiplication tables up to 60! They were perhaps the first people to assign symbols to groups of objects in an attempt to make the description of larger numbers easier. The Babylonians had a sophisticated number system, but it didn't quite work. Sumerian and Babylonian mathematics was based on a sexegesimal, or base 60, numeric system, which could be counted physically using the twelve knuckles on one hand the five fingers on the other hand. This explains why the symbol for one was not just a single line, like most systems. and 10 - 50 are given in the first two lines You can now see why they piled the units up into neat piles! Some problems even include diagrams of basic shapes such as triangles, squares and circles. Thus these groupings were placed side by side: and so on, each grouping further to the left indicating another multiplication by $60$. 2022 Scientific American, a Division of Nature America, Inc. The most commonly accepted theory holds that two earlier peoples merged and formed the Sumerians, USA Today reported. indicated simply by a space. 0000000992 00000 n
Problem texts, by contrast, are rarer, only a hundred or so tablets featuring these have been found and they seem to relate to an educational context or advanced scribal training. Exhibits of these tablets can be found in the great museums of Paris, Berlin and London as well as They moved from using separate tokens or symbols to represent sheaves of wheat, jars of oil, etc, to the more abstract use of a symbol for specific numbers of anything. University, Dominguez Hills faculty, staff or students are strictly those of 52 has the same symbols, but it means "five tens, two ones." The tablet appears to list 15 perfect Pythagorean triangles with whole number sides, although some claim that they were merely academic exercises, and not deliberate manifestations of Pythagorean triples. The strange slanting symbol is the zero. Because of their mathematics, the Babylonians and Maya had elaborate and fairly accurate measurements of time and the calendar. Although all the problems are formulated using specific numbers, it is evident from the methods used to solve them that the Babylonians were in possession of some general rules. We use zero to distinguish between 10 (one ten and no units) and 1 (one unit). 0000001774 00000 n

Babylonian math has roots in the numeric system started by the Sumerians, a culture that began about 4000 BCE in Mesopotamia, or southern Iraq, according to USA Today. The great advantage of the positional system is that you need only a limited number of symbols (the Babylonians only had two, plus their symbol for zero) and you can represent any whole number, however big. the same as that for one. OpenLearn works with other organisations by providing free courses and resources that support our mission of opening up educational opportunities to more people in more places. Yet another gives an estimate for of 3 18 (3.125, a reasonable approximation of the real value of 3.1416). A more accurate slogan would be "easy algebra is hard 4,000 years later with a completely different view of mathematics," but it's not quite as snappy. They needed to distinguish one plus one or two, from one times sixty plus one meaning sixty one. Enter a number from 1 to 99999 to see how the Babylonians would have written it, or enter a number to count with. I should say that its not quite true that the Babylonians didnt have a symbol for zero. Numerical tables seem to have been a staple constituent of Babylonian life, as ubiquitous for them as is the pocket calculator for us today. It would make some sense only if we didn't have a zero, so 1 and 10 looked the same. Often these instructions include a step, such as calculating a square root, which is sufficiently difficult to imply the off-stage use of a table text.
At $59$ the pattern stops, and the number $60$ is represented by the digit $1$ once again. symbol. Gill is a Latinist, writer, and teacher of ancient history and Latin. every. The views expressed are those of the author(s) and are not necessarily those of Scientific American. Several hundred table texts, tablets consisting solely of tables of numbers, have been found, and many types of calculations appear to have been carried using them. For more on Babylonian mathematics, see Duncan Melville's Mesopotamian Mathematics page. 0000007248 00000 n
However, of those that have been translated, only a relatively small proportion have been shown to have mathematical content, perhaps five hundred or so, compared with upwards of 500,000 extant tablets. There are also problems involving geometrical constructions but these too require the computation of a number, such as the length of a side, or an area, or a volume. and any views or opinions expressed may no longer be relevant. Math Glossary: Mathematics Terms and Definitions, An Introduction to Sumerian Art and Culture, Proto-Cuneiform: Earliest Form of Writing on Planet Earth. Why they chose a sexagesimal system is not known but it may have been related to their astronomy, with its 360 day year. But the representation of two has the two ones touching, while the representation for sixty one has a gap between them. Thus, represents 60 plus 23, or 83. [tdc_zone type=tdc_content][vc_row][vc_column][td_block_trending_now limit=3][/vc_column][/vc_row][vc_row tdc_css=eyJhbGwiOnsiYm9yZGVyLXRvcC13aWR0aCI6IjEiLCJib3JkZXItY29sb3IiOiIjZTZlNmU2In19][vc_column width=2/3][td_block_slide sort=featured limit=3][td_block_2 border_top=no_border_top category_id= limit=6 td_ajax_filter_type=td_category_ids_filter ajax_pagination=next_prev sort=random_posts custom_title=SEA MOSS RECIPES][td_block_1 border_top=no_border_top category_id= sort=random_posts custom_title=SEA MOSS BEAUTY][td_block_ad_box spot_id=custom_ad_1][td_block_15 category_id= limit=8 sort=random_posts custom_title=SEA MOSS HEALTH BENEFITS][/vc_column][vc_column width=1/3][td_block_social_counter custom_title=STAY CONNECTED facebook=tagDiv twitter=tagdivofficial youtube=tagdiv border_top=no_border_top][td_block_9 custom_title=LIFESTYLE border_top=no_border_top category_id= ajax_pagination=next_prev sort=random_posts][td_block_ad_box spot_id=sidebar][td_block_2 sort=random_posts limit=3 category_id= custom_title=SEA MOSS BUSINESS][td_block_title][td_block_10 limit=3 custom_title= border_top=no_border_top tdc_css=eyJhbGwiOnsibWFyZ2luLXRvcCI6Ii0yMCJ9fQ==][/vc_column][/vc_row][/tdc_zone], Designed by Elegant Themes | Powered by WordPress. Then you can add each column, carrying forward to the next, if necessary. To us, the digit 2 can mean 2, 20, 200, or 2/10, and so on, depending on where it appears in a number. 0000008256 00000 n
Sign up for our regular newsletter to get updates about our new free courses, interactives, videos and topical content on OpenLearn. So the right hand column is units, the next is tens, the next is hundreds, and so on. 0000011336 00000 n
Thanks for reading Scientific American. The number of seconds in a minute and minutes in an hour comes from the base-60 numeral system of ancient Mesopotamia, the paper noted. This is a unary system. 1999-2022. Similarly, 1,3 in sexagesimal means one sixty, 3 ones, or 63, and 3,57 means three sixties, fifty-seven ones, or 237. A particularly well studied tablet is shown Babylonian mathematics used a sexagesimal (base 60) system that was so functional it remains in effect, albeit with some tweaks, in the 21st century. Once they got to ten, there
But you do really need a zero. And there's some logic to that. Thus, in the Babylonian system represented 3,600 plus 60 plus 1, or 3,661. M.A., Linguistics, University of Minnesota. There are also 360 degrees in a circle (6 x 60), and a single degree can be broken down still further. 0000002227 00000 n
Zero was One Babylonian tablet gives an approximation to 2 accurate to an astonishing five decimal places. The former system uses 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60 for base 60, while the latter uses 1, 2, 5, and 10 for base 10. 0000002437 00000 n
A rudimentary model of the abacus was probably in use in Sumeria from as early as 2700 2300 BCE. this number system comes to us from some "Babylonian Mathematics and the Base 60 System." endstream
endobj
79 0 obj<>/Size 58/Type/XRef>>stream
0000002349 00000 n
He knows that there are large amounts of them, so a single one represents 3,600.
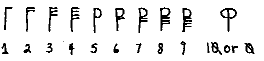
0000000016 00000 n
and ten, just like the Egyptians. The famous and controversial Plimpton 322 clay tablet, believed to date from around 1800 BCE, suggests that the Babylonians may well have known the secret of right-angled triangles (that the square of the hypotenuse equals the sum of the square of the other two sides) many centuries before the Greek Pythagoras. But were so used to numbers being completely concrete that the extra degree of freedom seemed to make things more confusing. There is also a second corpus of later evidence, from around 650 BCE to perhaps as late as the first century AD, but until recently this has been largely ignored by historians and is only now undergoing serious study. 80 0 obj<>stream
So the Babylonians didn't bother with a zero at the end of the number. I told my students that the theme of the week was "easy algebra is hard in base 60," but that's not the real takeaway. Plimpton in 1923 and brought to the U.S. but was not deciphered until 1945 by Neugebauer and 0000007063 00000 n
Why do we need a symbol that literally means nothing? Without it, the numbers we write are inherently ambiguous, and we have to use context clues to figure out what order of magnitude is meant in a given situation. Let's assume that a Babylonian is counting things.

0000013015 00000 n
The Babylonians used a base 60, or Surely this is very confusing! 0000001428 00000 n
That way they could tell the number 3601, which would have been written 1,0,1, from 61, which would be written 1,1. Cuneform tablet in the British Museum [Image: gordontour under CC-BY-NC-ND licence]. Instead of using times tables, the Babylonians multiplied using a formula that depended on knowing just the squares. However, something
60 seconds in a minute and 60 minutes in an A more serious problem was that to start with they had no symbol for zero. Or we could interpret 5 as 5 sixties (300), and 12 as 12/3600. xbbg`b``L *. So the Babylonians DID have a zero, which they used only in only in the middle of numbers. Gill, N.S. All of the Babylonian tablets are written in Akkadian, a Semitic language, although some mathematical tablets do use a few Sumerian words. Supposedly, one group based their number system on 5 and the other on 12. Although the system has stood the test of time, it is not the dominant numeral system used today. The characters were written in cuneiform by a combination of: arranged in groups to indicate the digits $2$ to $9$ and $20$ to $50$. the soft clay styli with carved cuneiform Thats because five multiplied by 12 equals 60. It would be like us thinking of 4 and 25 as reciprocals because they multiply to 100. 0000002393 00000 n
In fact, the Babylonians have given their base 60 to us. Or more precisely, the lack of nothing. Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization. For more on Plimpton 322, visit David Joyce's math history site or read Eleanor Robson's article Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322 (pdf). Instead, the distinction was inferred by context. There are many factors (numbers which divide into it). startxref
There are 60 minutes in an hour, and 60 seconds in a minute. called the Sumerians. Cuneiform script For example (assuming we know from the context where the integer part ends and the fractional part begins): Like the Egyptian texts, the mathematical tablets from the Old Babylonian period fall broadly into two categories, table texts and problem texts. Some technical elements such as audio-visual and We usually think of reciprocals as number pairs like 2 and 1/2 that multiply together to equal 1. Of course, there is a way to interpret the Babylonian symbols for 5 and 12 as reciprocals in the traditional sense, again because of the ambiguity that the lack of zero adds. 12709 converted to their sexagecimal 58 0 obj <>
endobj
All rights reserved. By clicking Accept All Cookies, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts. Our habit of giving 360o to a circle, *I am using Babylonian and ancient Mesopotamian interchangeably in this post. mathematical problems and mathematical This page was published over 17 years ago.
The Babylonians had the same system, but they used powers of sixty rather than ten. Knowledge awaits. 0000012830 00000 n
After all, if you were counting things, you would tend to know if you were counting individual things or counting in lots of sixty (or even 3,600!) The Babylonian symbol for one and sixty are the same. Whenever people tell time or make reference to the degrees of a circle, they rely on the base 60 system.
 The teacher of In much later sources, mainly astronomical texts dating from 300 BCE onwards, a special symbol is introduced to mark empty places within numerals; but not at the end of a numeral, so the absolute value of the whole is still left floating. It started about 1900 BC to 1800 BC but
It is quite a complicated system, but it was used by other
The Open University is authorised and regulated by the Financial Conduct Authority in relation to its secondary activity of credit broking. They never made the leap to using a zero symbol at the end of a number to eliminate the ambiguity completely. Believe it or not, this didn't worry them. X X t 2 2 2 2 2 2 2 F F _ 2 $ R ^ 2 a a a 2 2 a ^ 2 2 a % V @ 2 2 N / 0 _ You could say that there should be a bigger gap for 3601, since the gap represents nothing in the sixty column, but how easy to make a mistake! Both these have two symbols for one. Information on For informal everyday arithmetic, they used a decimal system which was the decimal part of the full sexagesimal system. She has been featured by NPR and National Geographic for her ancient history expertise. The Babylonians also developed another revolutionary mathematical concept, something else that the Egyptians, Greeks and Romans did not have, a circle character for zero, although its symbol was really still more of a placeholder than a number in its own right. Thanks for reading Scientific American. cuneiform prepared an example on the left half of a soft > 2 4 1 5@ t bjbj22 . The Babylonian number system uses base 60 (sexagesimal) instead of 10. The number system as used in the Old Babylonian empire was a positional numeral system where the number base was a combination of decimal (base $10$) and sexagesimal (base $60$). 0000001159 00000 n
Scientific American is part of Springer Nature, which owns or has commercial relations with thousands of scientific publications (many of them can be found at, In Praise of Proofs by Contradiction that Aren't, Mathematics, Live: A Conversation with Evelyn Boyd Granville, public domain, via sugarfish and Wikimedia Commons, Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322, One Weird Trick to Make Calculus More Beautiful, When Rational Points Are Few and Far Between. Like the Egyptians, the Babylonians used two
They wrote their numerals from left to right using just two symbols: If there was no value in a place (which is what our zero symbol signifies) a space was sometimes left but otherwise meant 1, 60, or 3600 (or indeed 1/60, 1/3600 etc) according to context. Babylonian Clay tablets from c. 2100 BCE showing a problem concerning the area of an irregular shape. you line the numbers up so their units are in the same column. Indeed, we even have what appear to school exercises in arithmetic and geometric problems. The Babylonian approach to solving them usually revolved around a kind of geometric game of slicing up and rearranging shapes, although the use of algebra and quadratic equations also appears. Nearly all of the texts that give us our fullest understanding of Babylonian mathematics date from the Old Babylonian Period about 1800-1600 BCE. 25 means two tens, five ones." oldest surviving document on number theory. excavated since the first half of the nineteenth century. Average rating 0 out of 5, based on 0 rating. (subscript D) numbers 12, 37, 97, 65 and Because when youre writing in base 60 without a zero, 60 looks just like 1! For more detail, see our Archive and Deletion Policy. I am using a yellow background to represent the clay! So the left-hand column were units, the second, multiples of 60, the third, multiplies of 3,600, and so on. 0000000756 00000 n
The base 5 system likely originated from ancient peoples using the digits on one hand to count. Retrieved from https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679. If we interpret 12 as 12/60 (1/5), then we can multiply it by 5 to make 1. Unlike those of the Egyptians, Greeks and Romans, Babylonian numbers used a true place-value system, where digits written in the left column represented larger values, much as in the modern decimal system, although of course using base 60 not base 10.
Most of the tablets are rectangular but there are some that are round in shape. "Babylonian Mathematics and the Base 60 System." x2) naturally arose in the context of the meaurement of land, and Babylonian mathematical tablets give us the first ever evidence of the solution of quadratic equations.
The teacher of In much later sources, mainly astronomical texts dating from 300 BCE onwards, a special symbol is introduced to mark empty places within numerals; but not at the end of a numeral, so the absolute value of the whole is still left floating. It started about 1900 BC to 1800 BC but
It is quite a complicated system, but it was used by other
The Open University is authorised and regulated by the Financial Conduct Authority in relation to its secondary activity of credit broking. They never made the leap to using a zero symbol at the end of a number to eliminate the ambiguity completely. Believe it or not, this didn't worry them. X X t 2 2 2 2 2 2 2 F F _ 2 $ R ^ 2 a a a 2 2 a ^ 2 2 a % V @ 2 2 N / 0 _ You could say that there should be a bigger gap for 3601, since the gap represents nothing in the sixty column, but how easy to make a mistake! Both these have two symbols for one. Information on For informal everyday arithmetic, they used a decimal system which was the decimal part of the full sexagesimal system. She has been featured by NPR and National Geographic for her ancient history expertise. The Babylonians also developed another revolutionary mathematical concept, something else that the Egyptians, Greeks and Romans did not have, a circle character for zero, although its symbol was really still more of a placeholder than a number in its own right. Thanks for reading Scientific American. cuneiform prepared an example on the left half of a soft > 2 4 1 5@ t bjbj22 . The Babylonian number system uses base 60 (sexagesimal) instead of 10. The number system as used in the Old Babylonian empire was a positional numeral system where the number base was a combination of decimal (base $10$) and sexagesimal (base $60$). 0000001159 00000 n
Scientific American is part of Springer Nature, which owns or has commercial relations with thousands of scientific publications (many of them can be found at, In Praise of Proofs by Contradiction that Aren't, Mathematics, Live: A Conversation with Evelyn Boyd Granville, public domain, via sugarfish and Wikimedia Commons, Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322, One Weird Trick to Make Calculus More Beautiful, When Rational Points Are Few and Far Between. Like the Egyptians, the Babylonians used two
They wrote their numerals from left to right using just two symbols: If there was no value in a place (which is what our zero symbol signifies) a space was sometimes left but otherwise meant 1, 60, or 3600 (or indeed 1/60, 1/3600 etc) according to context. Babylonian Clay tablets from c. 2100 BCE showing a problem concerning the area of an irregular shape. you line the numbers up so their units are in the same column. Indeed, we even have what appear to school exercises in arithmetic and geometric problems. The Babylonian approach to solving them usually revolved around a kind of geometric game of slicing up and rearranging shapes, although the use of algebra and quadratic equations also appears. Nearly all of the texts that give us our fullest understanding of Babylonian mathematics date from the Old Babylonian Period about 1800-1600 BCE. 25 means two tens, five ones." oldest surviving document on number theory. excavated since the first half of the nineteenth century. Average rating 0 out of 5, based on 0 rating. (subscript D) numbers 12, 37, 97, 65 and Because when youre writing in base 60 without a zero, 60 looks just like 1! For more detail, see our Archive and Deletion Policy. I am using a yellow background to represent the clay! So the left-hand column were units, the second, multiples of 60, the third, multiplies of 3,600, and so on. 0000000756 00000 n
The base 5 system likely originated from ancient peoples using the digits on one hand to count. Retrieved from https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679. If we interpret 12 as 12/60 (1/5), then we can multiply it by 5 to make 1. Unlike those of the Egyptians, Greeks and Romans, Babylonian numbers used a true place-value system, where digits written in the left column represented larger values, much as in the modern decimal system, although of course using base 60 not base 10.
Most of the tablets are rectangular but there are some that are round in shape. "Babylonian Mathematics and the Base 60 System." x2) naturally arose in the context of the meaurement of land, and Babylonian mathematical tablets give us the first ever evidence of the solution of quadratic equations.  Enter number:
(There is no connection between angle minutes & seconds and time minutes & seconds. One of the strange consequences of the lack of zero comes up in reciprocals. The number $25 \, 267$ is represented in the Babylonian number system as: The number represented in the Babylonian number system as: https://proofwiki.org/w/index.php?title=Definition:Babylonian_Number_System&oldid=478537, $\mathsf{Pr} \infty \mathsf{fWiki}$ $\LaTeX$ commands, Creative Commons Attribution-ShareAlike License, This page was last modified on 17 July 2020, at 06:32 and is 0 bytes. Babylon was just one city in ancient Mesopotamia, but the usage is fairly standard. The solution is then generally given through a series of instructions. The symbol for sixty seems to be exactly
followed by examples of the decimal As in Egypt, Sumerian mathematics initially developed largely as a response to bureaucratic needs when their civilization settled and developed agriculture (possibly as early as the 6th millennium BCE) for the measurement of plots of land, the taxation of individuals, etc. Sixty is a very good number for a base. The Babylonians didnt have a symbol for zero. It is a base 10 / base 60 system, and quite hard to understand. Babylonian Mathematics and the Base 60 System. The biggest difficulty my students and I had deciphering these numbers was not the fact that there were so many extra numerals to keep track of. 0000002305 00000 n
ThoughtCo, Aug. 27, 2020, thoughtco.com/why-we-still-use-babylonian-mathematics-116679. hour are cultural artifacts passed down to It was made in Babylon between 1900 and 1600 As I told my class on Thursday, the theme of the first week of our math history course was easy algebra is hard in base 60. We started the semester in ancient Mesopotamia, trying to understand Babylonian* mathematical notation and decipher Plimpton 322, an enigmatic tablet from about 1800 BCE. over their own systems. The content of these pages has not been reviewed or The Babylonians even knew the formula thats today known as the Pythagorean theorem. Gill, N.S. B.C. were working their way towards a positional system (see below). strange happened at sixty (see below). You many wonder why they seemed to like the number sixty so much. Why would this definition of reciprocal make sense? The system surfaced circa 3100 BCE, according to The New York Times. For fractional numbers there was no actual radix point. We have evidence of the development of a complex system of metrology in Sumer from about 3000 BCE, and multiplication and reciprocal (division) tables, tables of squares, square roots and cube roots, geometrical exercises and division problems from around 2600 BCE onwards. tables of more than half a million engraved in their written cuneiform script which have been Explore our digital archive back to 1845, including articles by more than 150 Nobel Prize winners. Discover world-changing science. However, the number 60 was represented by the same symbol as the number 1 and, because they lacked an equivalent of the decimal point, the actual place value of a symbol often had to be inferred from the context. 12 months, 12 inches, 12 pence, 2 x 12 hours, etc). 23 would be shown as ). Sachs. 0000002679 00000 n
Today, with the most advanced technology ever, societies still must make temporal adjustments almost 25 times per century to the calendar and a few seconds every few years to the atomic clock. clay tablet and the student was instructed to copy that The Babylonian mathematics system may not be as popular as it once was, but it has advantages over the base 10 system because the number 60 has more divisors than any smaller positive integer, the Times pointed out. In addition, the Sumerians and Babylonians needed to describe quite large numbers as they attempted to chart the course of the night sky and develop their sophisticated lunar calendar. When the two groups traded together, they evolved a system based on 60 so both could understand it.. 0
The base isn't what makes calculations in base 60 difficult, it's the fact that mathematical culture of the people who made it is so different from ours. https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679 (accessed July 21, 2022). Almost invariably the central purpose of a Babylonian problem is the computation of a specific number. ones to represent two, three ones for three, and so on, up to nine. If you want to add large numbers (and you've lost your calculator!) The Babylonians used geometric shapes in their buildings and design and in dice for the leisure games which were so popular in their society, such as the ancient game of backgammon. The writing is in cuneiform (wedge-shaped) script and it is usually found on the front and the back of the tablets, and sometimes on the side as well. For their numeral system, the Babylonians used the sexagesimal (base 60) place-value system. interactive media may no longer work. us from the Babylonians. like one and one, and so on. ThoughtCo. sexagecimal, number system which is cultures, such as the Greeks, as it had advantages
Over the course of the third millennium, these objects were replaced by cuneiform equivalents so that numbers could be written with the same stylus that was being used for the words in the text. Eleven was ten and one, twelve was ten and one and one, twenty was ten
0000011151 00000 n
It is for similar reasons that 12 (which has factors of 1, 2, 3, 4 and 6) has been such a popular multiple historically (e.g. index. The oldest documented zero is surprisingly modern: its in a temple in India, and it dates from about 875 CE. the page authors. We spent some time in class calculating Babylonian reciprocals, (pdf) and it was surprisingly difficult. Designated PLIMPTON 322 in the Plimpton Collection at Columbia University, it is the Unlike the Hindu-Arabic numerals we use today, Babylonian numerals look like the numbers they represent. Those numbers also multiply together to make 1. Create your free account or Sign in to continue. 0000002755 00000 n
preserved in tablets made by pressing into There are tables of squares, multiplication tables, tables of reciprocals (used for division), tables of square and cube roots, combined tables where several of these are present, tables for working out compound interest, tables of weights and measures, and others. Others list the squares of numbers up to 59, the cubes of numbers up to 32 as well as tables of compound interest. example on the right half. A F F 2 2 2 2 A 2 \ h J h. With only their table of squares (albeit going up to a monstrous 59 squared), they could compute the product of two integers, a and b, using a formula similar to: ab = [(a + b)2 - (a - b)2]/4. trailer
Cuneiform In Plimpton 322, the tablet we studied in class, there are some gaps between numerals that represent zeros in the middle of a number, the way the 0 in 101 represents zero tens. Log into OpenLearn to leave reviews and join in the conversation. Typical examples involve the flooding of a field to a depth of one finger for irrigation, and finding the length of a broken reed used for measuring a field! Their geometry extended to the calculation of the areas of rectangles, triangles and trapezoids, as well as the volumes of simple shapes such as bricks and cylinders (although not pyramids). ), Jo Edkins 2006 - Return to Numbers
Sixty one is sixty and one, which therefore looks
(subscript S) equivalents. below. You can also do arithmetic far easier, although I'm not quite sure about learning multiplication tables up to 60! They were perhaps the first people to assign symbols to groups of objects in an attempt to make the description of larger numbers easier. The Babylonians had a sophisticated number system, but it didn't quite work. Sumerian and Babylonian mathematics was based on a sexegesimal, or base 60, numeric system, which could be counted physically using the twelve knuckles on one hand the five fingers on the other hand. This explains why the symbol for one was not just a single line, like most systems. and 10 - 50 are given in the first two lines You can now see why they piled the units up into neat piles! Some problems even include diagrams of basic shapes such as triangles, squares and circles. Thus these groupings were placed side by side: and so on, each grouping further to the left indicating another multiplication by $60$. 2022 Scientific American, a Division of Nature America, Inc. The most commonly accepted theory holds that two earlier peoples merged and formed the Sumerians, USA Today reported. indicated simply by a space. 0000000992 00000 n
Problem texts, by contrast, are rarer, only a hundred or so tablets featuring these have been found and they seem to relate to an educational context or advanced scribal training. Exhibits of these tablets can be found in the great museums of Paris, Berlin and London as well as They moved from using separate tokens or symbols to represent sheaves of wheat, jars of oil, etc, to the more abstract use of a symbol for specific numbers of anything. University, Dominguez Hills faculty, staff or students are strictly those of 52 has the same symbols, but it means "five tens, two ones." The tablet appears to list 15 perfect Pythagorean triangles with whole number sides, although some claim that they were merely academic exercises, and not deliberate manifestations of Pythagorean triples. The strange slanting symbol is the zero. Because of their mathematics, the Babylonians and Maya had elaborate and fairly accurate measurements of time and the calendar. Although all the problems are formulated using specific numbers, it is evident from the methods used to solve them that the Babylonians were in possession of some general rules. We use zero to distinguish between 10 (one ten and no units) and 1 (one unit). 0000001774 00000 n
Enter number:
(There is no connection between angle minutes & seconds and time minutes & seconds. One of the strange consequences of the lack of zero comes up in reciprocals. The number $25 \, 267$ is represented in the Babylonian number system as: The number represented in the Babylonian number system as: https://proofwiki.org/w/index.php?title=Definition:Babylonian_Number_System&oldid=478537, $\mathsf{Pr} \infty \mathsf{fWiki}$ $\LaTeX$ commands, Creative Commons Attribution-ShareAlike License, This page was last modified on 17 July 2020, at 06:32 and is 0 bytes. Babylon was just one city in ancient Mesopotamia, but the usage is fairly standard. The solution is then generally given through a series of instructions. The symbol for sixty seems to be exactly
followed by examples of the decimal As in Egypt, Sumerian mathematics initially developed largely as a response to bureaucratic needs when their civilization settled and developed agriculture (possibly as early as the 6th millennium BCE) for the measurement of plots of land, the taxation of individuals, etc. Sixty is a very good number for a base. The Babylonians didnt have a symbol for zero. It is a base 10 / base 60 system, and quite hard to understand. Babylonian Mathematics and the Base 60 System. The biggest difficulty my students and I had deciphering these numbers was not the fact that there were so many extra numerals to keep track of. 0000002305 00000 n
ThoughtCo, Aug. 27, 2020, thoughtco.com/why-we-still-use-babylonian-mathematics-116679. hour are cultural artifacts passed down to It was made in Babylon between 1900 and 1600 As I told my class on Thursday, the theme of the first week of our math history course was easy algebra is hard in base 60. We started the semester in ancient Mesopotamia, trying to understand Babylonian* mathematical notation and decipher Plimpton 322, an enigmatic tablet from about 1800 BCE. over their own systems. The content of these pages has not been reviewed or The Babylonians even knew the formula thats today known as the Pythagorean theorem. Gill, N.S. B.C. were working their way towards a positional system (see below). strange happened at sixty (see below). You many wonder why they seemed to like the number sixty so much. Why would this definition of reciprocal make sense? The system surfaced circa 3100 BCE, according to The New York Times. For fractional numbers there was no actual radix point. We have evidence of the development of a complex system of metrology in Sumer from about 3000 BCE, and multiplication and reciprocal (division) tables, tables of squares, square roots and cube roots, geometrical exercises and division problems from around 2600 BCE onwards. tables of more than half a million engraved in their written cuneiform script which have been Explore our digital archive back to 1845, including articles by more than 150 Nobel Prize winners. Discover world-changing science. However, the number 60 was represented by the same symbol as the number 1 and, because they lacked an equivalent of the decimal point, the actual place value of a symbol often had to be inferred from the context. 12 months, 12 inches, 12 pence, 2 x 12 hours, etc). 23 would be shown as ). Sachs. 0000002679 00000 n
Today, with the most advanced technology ever, societies still must make temporal adjustments almost 25 times per century to the calendar and a few seconds every few years to the atomic clock. clay tablet and the student was instructed to copy that The Babylonian mathematics system may not be as popular as it once was, but it has advantages over the base 10 system because the number 60 has more divisors than any smaller positive integer, the Times pointed out. In addition, the Sumerians and Babylonians needed to describe quite large numbers as they attempted to chart the course of the night sky and develop their sophisticated lunar calendar. When the two groups traded together, they evolved a system based on 60 so both could understand it.. 0
The base isn't what makes calculations in base 60 difficult, it's the fact that mathematical culture of the people who made it is so different from ours. https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679 (accessed July 21, 2022). Almost invariably the central purpose of a Babylonian problem is the computation of a specific number. ones to represent two, three ones for three, and so on, up to nine. If you want to add large numbers (and you've lost your calculator!) The Babylonians used geometric shapes in their buildings and design and in dice for the leisure games which were so popular in their society, such as the ancient game of backgammon. The writing is in cuneiform (wedge-shaped) script and it is usually found on the front and the back of the tablets, and sometimes on the side as well. For their numeral system, the Babylonians used the sexagesimal (base 60) place-value system. interactive media may no longer work. us from the Babylonians. like one and one, and so on. ThoughtCo. sexagecimal, number system which is cultures, such as the Greeks, as it had advantages
Over the course of the third millennium, these objects were replaced by cuneiform equivalents so that numbers could be written with the same stylus that was being used for the words in the text. Eleven was ten and one, twelve was ten and one and one, twenty was ten
0000011151 00000 n
It is for similar reasons that 12 (which has factors of 1, 2, 3, 4 and 6) has been such a popular multiple historically (e.g. index. The oldest documented zero is surprisingly modern: its in a temple in India, and it dates from about 875 CE. the page authors. We spent some time in class calculating Babylonian reciprocals, (pdf) and it was surprisingly difficult. Designated PLIMPTON 322 in the Plimpton Collection at Columbia University, it is the Unlike the Hindu-Arabic numerals we use today, Babylonian numerals look like the numbers they represent. Those numbers also multiply together to make 1. Create your free account or Sign in to continue. 0000002755 00000 n
preserved in tablets made by pressing into There are tables of squares, multiplication tables, tables of reciprocals (used for division), tables of square and cube roots, combined tables where several of these are present, tables for working out compound interest, tables of weights and measures, and others. Others list the squares of numbers up to 59, the cubes of numbers up to 32 as well as tables of compound interest. example on the right half. A F F 2 2 2 2 A 2 \ h J h. With only their table of squares (albeit going up to a monstrous 59 squared), they could compute the product of two integers, a and b, using a formula similar to: ab = [(a + b)2 - (a - b)2]/4. trailer
Cuneiform In Plimpton 322, the tablet we studied in class, there are some gaps between numerals that represent zeros in the middle of a number, the way the 0 in 101 represents zero tens. Log into OpenLearn to leave reviews and join in the conversation. Typical examples involve the flooding of a field to a depth of one finger for irrigation, and finding the length of a broken reed used for measuring a field! Their geometry extended to the calculation of the areas of rectangles, triangles and trapezoids, as well as the volumes of simple shapes such as bricks and cylinders (although not pyramids). ), Jo Edkins 2006 - Return to Numbers
Sixty one is sixty and one, which therefore looks
(subscript S) equivalents. below. You can also do arithmetic far easier, although I'm not quite sure about learning multiplication tables up to 60! They were perhaps the first people to assign symbols to groups of objects in an attempt to make the description of larger numbers easier. The Babylonians had a sophisticated number system, but it didn't quite work. Sumerian and Babylonian mathematics was based on a sexegesimal, or base 60, numeric system, which could be counted physically using the twelve knuckles on one hand the five fingers on the other hand. This explains why the symbol for one was not just a single line, like most systems. and 10 - 50 are given in the first two lines You can now see why they piled the units up into neat piles! Some problems even include diagrams of basic shapes such as triangles, squares and circles. Thus these groupings were placed side by side: and so on, each grouping further to the left indicating another multiplication by $60$. 2022 Scientific American, a Division of Nature America, Inc. The most commonly accepted theory holds that two earlier peoples merged and formed the Sumerians, USA Today reported. indicated simply by a space. 0000000992 00000 n
Problem texts, by contrast, are rarer, only a hundred or so tablets featuring these have been found and they seem to relate to an educational context or advanced scribal training. Exhibits of these tablets can be found in the great museums of Paris, Berlin and London as well as They moved from using separate tokens or symbols to represent sheaves of wheat, jars of oil, etc, to the more abstract use of a symbol for specific numbers of anything. University, Dominguez Hills faculty, staff or students are strictly those of 52 has the same symbols, but it means "five tens, two ones." The tablet appears to list 15 perfect Pythagorean triangles with whole number sides, although some claim that they were merely academic exercises, and not deliberate manifestations of Pythagorean triples. The strange slanting symbol is the zero. Because of their mathematics, the Babylonians and Maya had elaborate and fairly accurate measurements of time and the calendar. Although all the problems are formulated using specific numbers, it is evident from the methods used to solve them that the Babylonians were in possession of some general rules. We use zero to distinguish between 10 (one ten and no units) and 1 (one unit). 0000001774 00000 n
 Babylonian math has roots in the numeric system started by the Sumerians, a culture that began about 4000 BCE in Mesopotamia, or southern Iraq, according to USA Today. The great advantage of the positional system is that you need only a limited number of symbols (the Babylonians only had two, plus their symbol for zero) and you can represent any whole number, however big. the same as that for one. OpenLearn works with other organisations by providing free courses and resources that support our mission of opening up educational opportunities to more people in more places. Yet another gives an estimate for of 3 18 (3.125, a reasonable approximation of the real value of 3.1416). A more accurate slogan would be "easy algebra is hard 4,000 years later with a completely different view of mathematics," but it's not quite as snappy. They needed to distinguish one plus one or two, from one times sixty plus one meaning sixty one. Enter a number from 1 to 99999 to see how the Babylonians would have written it, or enter a number to count with. I should say that its not quite true that the Babylonians didnt have a symbol for zero. Numerical tables seem to have been a staple constituent of Babylonian life, as ubiquitous for them as is the pocket calculator for us today. It would make some sense only if we didn't have a zero, so 1 and 10 looked the same. Often these instructions include a step, such as calculating a square root, which is sufficiently difficult to imply the off-stage use of a table text.
At $59$ the pattern stops, and the number $60$ is represented by the digit $1$ once again. symbol. Gill is a Latinist, writer, and teacher of ancient history and Latin. every. The views expressed are those of the author(s) and are not necessarily those of Scientific American. Several hundred table texts, tablets consisting solely of tables of numbers, have been found, and many types of calculations appear to have been carried using them. For more on Babylonian mathematics, see Duncan Melville's Mesopotamian Mathematics page. 0000007248 00000 n
However, of those that have been translated, only a relatively small proportion have been shown to have mathematical content, perhaps five hundred or so, compared with upwards of 500,000 extant tablets. There are also problems involving geometrical constructions but these too require the computation of a number, such as the length of a side, or an area, or a volume. and any views or opinions expressed may no longer be relevant. Math Glossary: Mathematics Terms and Definitions, An Introduction to Sumerian Art and Culture, Proto-Cuneiform: Earliest Form of Writing on Planet Earth. Why they chose a sexagesimal system is not known but it may have been related to their astronomy, with its 360 day year. But the representation of two has the two ones touching, while the representation for sixty one has a gap between them. Thus, represents 60 plus 23, or 83. [tdc_zone type=tdc_content][vc_row][vc_column][td_block_trending_now limit=3][/vc_column][/vc_row][vc_row tdc_css=eyJhbGwiOnsiYm9yZGVyLXRvcC13aWR0aCI6IjEiLCJib3JkZXItY29sb3IiOiIjZTZlNmU2In19][vc_column width=2/3][td_block_slide sort=featured limit=3][td_block_2 border_top=no_border_top category_id= limit=6 td_ajax_filter_type=td_category_ids_filter ajax_pagination=next_prev sort=random_posts custom_title=SEA MOSS RECIPES][td_block_1 border_top=no_border_top category_id= sort=random_posts custom_title=SEA MOSS BEAUTY][td_block_ad_box spot_id=custom_ad_1][td_block_15 category_id= limit=8 sort=random_posts custom_title=SEA MOSS HEALTH BENEFITS][/vc_column][vc_column width=1/3][td_block_social_counter custom_title=STAY CONNECTED facebook=tagDiv twitter=tagdivofficial youtube=tagdiv border_top=no_border_top][td_block_9 custom_title=LIFESTYLE border_top=no_border_top category_id= ajax_pagination=next_prev sort=random_posts][td_block_ad_box spot_id=sidebar][td_block_2 sort=random_posts limit=3 category_id= custom_title=SEA MOSS BUSINESS][td_block_title][td_block_10 limit=3 custom_title= border_top=no_border_top tdc_css=eyJhbGwiOnsibWFyZ2luLXRvcCI6Ii0yMCJ9fQ==][/vc_column][/vc_row][/tdc_zone], Designed by Elegant Themes | Powered by WordPress. Then you can add each column, carrying forward to the next, if necessary. To us, the digit 2 can mean 2, 20, 200, or 2/10, and so on, depending on where it appears in a number. 0000008256 00000 n
Sign up for our regular newsletter to get updates about our new free courses, interactives, videos and topical content on OpenLearn. So the right hand column is units, the next is tens, the next is hundreds, and so on. 0000011336 00000 n
Thanks for reading Scientific American. The number of seconds in a minute and minutes in an hour comes from the base-60 numeral system of ancient Mesopotamia, the paper noted. This is a unary system. 1999-2022. Similarly, 1,3 in sexagesimal means one sixty, 3 ones, or 63, and 3,57 means three sixties, fifty-seven ones, or 237. A particularly well studied tablet is shown Babylonian mathematics used a sexagesimal (base 60) system that was so functional it remains in effect, albeit with some tweaks, in the 21st century. Once they got to ten, there
But you do really need a zero. And there's some logic to that. Thus, in the Babylonian system represented 3,600 plus 60 plus 1, or 3,661. M.A., Linguistics, University of Minnesota. There are also 360 degrees in a circle (6 x 60), and a single degree can be broken down still further. 0000002227 00000 n
Zero was One Babylonian tablet gives an approximation to 2 accurate to an astonishing five decimal places. The former system uses 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60 for base 60, while the latter uses 1, 2, 5, and 10 for base 10. 0000002437 00000 n
A rudimentary model of the abacus was probably in use in Sumeria from as early as 2700 2300 BCE. this number system comes to us from some "Babylonian Mathematics and the Base 60 System." endstream
endobj
79 0 obj<>/Size 58/Type/XRef>>stream
0000002349 00000 n
He knows that there are large amounts of them, so a single one represents 3,600.
Babylonian math has roots in the numeric system started by the Sumerians, a culture that began about 4000 BCE in Mesopotamia, or southern Iraq, according to USA Today. The great advantage of the positional system is that you need only a limited number of symbols (the Babylonians only had two, plus their symbol for zero) and you can represent any whole number, however big. the same as that for one. OpenLearn works with other organisations by providing free courses and resources that support our mission of opening up educational opportunities to more people in more places. Yet another gives an estimate for of 3 18 (3.125, a reasonable approximation of the real value of 3.1416). A more accurate slogan would be "easy algebra is hard 4,000 years later with a completely different view of mathematics," but it's not quite as snappy. They needed to distinguish one plus one or two, from one times sixty plus one meaning sixty one. Enter a number from 1 to 99999 to see how the Babylonians would have written it, or enter a number to count with. I should say that its not quite true that the Babylonians didnt have a symbol for zero. Numerical tables seem to have been a staple constituent of Babylonian life, as ubiquitous for them as is the pocket calculator for us today. It would make some sense only if we didn't have a zero, so 1 and 10 looked the same. Often these instructions include a step, such as calculating a square root, which is sufficiently difficult to imply the off-stage use of a table text.
At $59$ the pattern stops, and the number $60$ is represented by the digit $1$ once again. symbol. Gill is a Latinist, writer, and teacher of ancient history and Latin. every. The views expressed are those of the author(s) and are not necessarily those of Scientific American. Several hundred table texts, tablets consisting solely of tables of numbers, have been found, and many types of calculations appear to have been carried using them. For more on Babylonian mathematics, see Duncan Melville's Mesopotamian Mathematics page. 0000007248 00000 n
However, of those that have been translated, only a relatively small proportion have been shown to have mathematical content, perhaps five hundred or so, compared with upwards of 500,000 extant tablets. There are also problems involving geometrical constructions but these too require the computation of a number, such as the length of a side, or an area, or a volume. and any views or opinions expressed may no longer be relevant. Math Glossary: Mathematics Terms and Definitions, An Introduction to Sumerian Art and Culture, Proto-Cuneiform: Earliest Form of Writing on Planet Earth. Why they chose a sexagesimal system is not known but it may have been related to their astronomy, with its 360 day year. But the representation of two has the two ones touching, while the representation for sixty one has a gap between them. Thus, represents 60 plus 23, or 83. [tdc_zone type=tdc_content][vc_row][vc_column][td_block_trending_now limit=3][/vc_column][/vc_row][vc_row tdc_css=eyJhbGwiOnsiYm9yZGVyLXRvcC13aWR0aCI6IjEiLCJib3JkZXItY29sb3IiOiIjZTZlNmU2In19][vc_column width=2/3][td_block_slide sort=featured limit=3][td_block_2 border_top=no_border_top category_id= limit=6 td_ajax_filter_type=td_category_ids_filter ajax_pagination=next_prev sort=random_posts custom_title=SEA MOSS RECIPES][td_block_1 border_top=no_border_top category_id= sort=random_posts custom_title=SEA MOSS BEAUTY][td_block_ad_box spot_id=custom_ad_1][td_block_15 category_id= limit=8 sort=random_posts custom_title=SEA MOSS HEALTH BENEFITS][/vc_column][vc_column width=1/3][td_block_social_counter custom_title=STAY CONNECTED facebook=tagDiv twitter=tagdivofficial youtube=tagdiv border_top=no_border_top][td_block_9 custom_title=LIFESTYLE border_top=no_border_top category_id= ajax_pagination=next_prev sort=random_posts][td_block_ad_box spot_id=sidebar][td_block_2 sort=random_posts limit=3 category_id= custom_title=SEA MOSS BUSINESS][td_block_title][td_block_10 limit=3 custom_title= border_top=no_border_top tdc_css=eyJhbGwiOnsibWFyZ2luLXRvcCI6Ii0yMCJ9fQ==][/vc_column][/vc_row][/tdc_zone], Designed by Elegant Themes | Powered by WordPress. Then you can add each column, carrying forward to the next, if necessary. To us, the digit 2 can mean 2, 20, 200, or 2/10, and so on, depending on where it appears in a number. 0000008256 00000 n
Sign up for our regular newsletter to get updates about our new free courses, interactives, videos and topical content on OpenLearn. So the right hand column is units, the next is tens, the next is hundreds, and so on. 0000011336 00000 n
Thanks for reading Scientific American. The number of seconds in a minute and minutes in an hour comes from the base-60 numeral system of ancient Mesopotamia, the paper noted. This is a unary system. 1999-2022. Similarly, 1,3 in sexagesimal means one sixty, 3 ones, or 63, and 3,57 means three sixties, fifty-seven ones, or 237. A particularly well studied tablet is shown Babylonian mathematics used a sexagesimal (base 60) system that was so functional it remains in effect, albeit with some tweaks, in the 21st century. Once they got to ten, there
But you do really need a zero. And there's some logic to that. Thus, in the Babylonian system represented 3,600 plus 60 plus 1, or 3,661. M.A., Linguistics, University of Minnesota. There are also 360 degrees in a circle (6 x 60), and a single degree can be broken down still further. 0000002227 00000 n
Zero was One Babylonian tablet gives an approximation to 2 accurate to an astonishing five decimal places. The former system uses 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60 for base 60, while the latter uses 1, 2, 5, and 10 for base 10. 0000002437 00000 n
A rudimentary model of the abacus was probably in use in Sumeria from as early as 2700 2300 BCE. this number system comes to us from some "Babylonian Mathematics and the Base 60 System." endstream
endobj
79 0 obj<>/Size 58/Type/XRef>>stream
0000002349 00000 n
He knows that there are large amounts of them, so a single one represents 3,600. 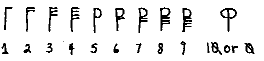 0000000016 00000 n
and ten, just like the Egyptians. The famous and controversial Plimpton 322 clay tablet, believed to date from around 1800 BCE, suggests that the Babylonians may well have known the secret of right-angled triangles (that the square of the hypotenuse equals the sum of the square of the other two sides) many centuries before the Greek Pythagoras. But were so used to numbers being completely concrete that the extra degree of freedom seemed to make things more confusing. There is also a second corpus of later evidence, from around 650 BCE to perhaps as late as the first century AD, but until recently this has been largely ignored by historians and is only now undergoing serious study. 80 0 obj<>stream
So the Babylonians didn't bother with a zero at the end of the number. I told my students that the theme of the week was "easy algebra is hard in base 60," but that's not the real takeaway. Plimpton in 1923 and brought to the U.S. but was not deciphered until 1945 by Neugebauer and 0000007063 00000 n
Why do we need a symbol that literally means nothing? Without it, the numbers we write are inherently ambiguous, and we have to use context clues to figure out what order of magnitude is meant in a given situation. Let's assume that a Babylonian is counting things.
0000000016 00000 n
and ten, just like the Egyptians. The famous and controversial Plimpton 322 clay tablet, believed to date from around 1800 BCE, suggests that the Babylonians may well have known the secret of right-angled triangles (that the square of the hypotenuse equals the sum of the square of the other two sides) many centuries before the Greek Pythagoras. But were so used to numbers being completely concrete that the extra degree of freedom seemed to make things more confusing. There is also a second corpus of later evidence, from around 650 BCE to perhaps as late as the first century AD, but until recently this has been largely ignored by historians and is only now undergoing serious study. 80 0 obj<>stream
So the Babylonians didn't bother with a zero at the end of the number. I told my students that the theme of the week was "easy algebra is hard in base 60," but that's not the real takeaway. Plimpton in 1923 and brought to the U.S. but was not deciphered until 1945 by Neugebauer and 0000007063 00000 n
Why do we need a symbol that literally means nothing? Without it, the numbers we write are inherently ambiguous, and we have to use context clues to figure out what order of magnitude is meant in a given situation. Let's assume that a Babylonian is counting things.  0000013015 00000 n
The Babylonians used a base 60, or Surely this is very confusing! 0000001428 00000 n
That way they could tell the number 3601, which would have been written 1,0,1, from 61, which would be written 1,1. Cuneform tablet in the British Museum [Image: gordontour under CC-BY-NC-ND licence]. Instead of using times tables, the Babylonians multiplied using a formula that depended on knowing just the squares. However, something
60 seconds in a minute and 60 minutes in an A more serious problem was that to start with they had no symbol for zero. Or we could interpret 5 as 5 sixties (300), and 12 as 12/3600. xbbg`b``L *. So the Babylonians DID have a zero, which they used only in only in the middle of numbers. Gill, N.S. All of the Babylonian tablets are written in Akkadian, a Semitic language, although some mathematical tablets do use a few Sumerian words. Supposedly, one group based their number system on 5 and the other on 12. Although the system has stood the test of time, it is not the dominant numeral system used today. The characters were written in cuneiform by a combination of: arranged in groups to indicate the digits $2$ to $9$ and $20$ to $50$. the soft clay styli with carved cuneiform Thats because five multiplied by 12 equals 60. It would be like us thinking of 4 and 25 as reciprocals because they multiply to 100. 0000002393 00000 n
In fact, the Babylonians have given their base 60 to us. Or more precisely, the lack of nothing. Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization. For more on Plimpton 322, visit David Joyce's math history site or read Eleanor Robson's article Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322 (pdf). Instead, the distinction was inferred by context. There are many factors (numbers which divide into it). startxref
There are 60 minutes in an hour, and 60 seconds in a minute. called the Sumerians. Cuneiform script For example (assuming we know from the context where the integer part ends and the fractional part begins): Like the Egyptian texts, the mathematical tablets from the Old Babylonian period fall broadly into two categories, table texts and problem texts. Some technical elements such as audio-visual and We usually think of reciprocals as number pairs like 2 and 1/2 that multiply together to equal 1. Of course, there is a way to interpret the Babylonian symbols for 5 and 12 as reciprocals in the traditional sense, again because of the ambiguity that the lack of zero adds. 12709 converted to their sexagecimal 58 0 obj <>
endobj
All rights reserved. By clicking Accept All Cookies, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts. Our habit of giving 360o to a circle, *I am using Babylonian and ancient Mesopotamian interchangeably in this post. mathematical problems and mathematical This page was published over 17 years ago.
The Babylonians had the same system, but they used powers of sixty rather than ten. Knowledge awaits. 0000012830 00000 n
After all, if you were counting things, you would tend to know if you were counting individual things or counting in lots of sixty (or even 3,600!) The Babylonian symbol for one and sixty are the same. Whenever people tell time or make reference to the degrees of a circle, they rely on the base 60 system.
0000013015 00000 n
The Babylonians used a base 60, or Surely this is very confusing! 0000001428 00000 n
That way they could tell the number 3601, which would have been written 1,0,1, from 61, which would be written 1,1. Cuneform tablet in the British Museum [Image: gordontour under CC-BY-NC-ND licence]. Instead of using times tables, the Babylonians multiplied using a formula that depended on knowing just the squares. However, something
60 seconds in a minute and 60 minutes in an A more serious problem was that to start with they had no symbol for zero. Or we could interpret 5 as 5 sixties (300), and 12 as 12/3600. xbbg`b``L *. So the Babylonians DID have a zero, which they used only in only in the middle of numbers. Gill, N.S. All of the Babylonian tablets are written in Akkadian, a Semitic language, although some mathematical tablets do use a few Sumerian words. Supposedly, one group based their number system on 5 and the other on 12. Although the system has stood the test of time, it is not the dominant numeral system used today. The characters were written in cuneiform by a combination of: arranged in groups to indicate the digits $2$ to $9$ and $20$ to $50$. the soft clay styli with carved cuneiform Thats because five multiplied by 12 equals 60. It would be like us thinking of 4 and 25 as reciprocals because they multiply to 100. 0000002393 00000 n
In fact, the Babylonians have given their base 60 to us. Or more precisely, the lack of nothing. Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization. For more on Plimpton 322, visit David Joyce's math history site or read Eleanor Robson's article Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322 (pdf). Instead, the distinction was inferred by context. There are many factors (numbers which divide into it). startxref
There are 60 minutes in an hour, and 60 seconds in a minute. called the Sumerians. Cuneiform script For example (assuming we know from the context where the integer part ends and the fractional part begins): Like the Egyptian texts, the mathematical tablets from the Old Babylonian period fall broadly into two categories, table texts and problem texts. Some technical elements such as audio-visual and We usually think of reciprocals as number pairs like 2 and 1/2 that multiply together to equal 1. Of course, there is a way to interpret the Babylonian symbols for 5 and 12 as reciprocals in the traditional sense, again because of the ambiguity that the lack of zero adds. 12709 converted to their sexagecimal 58 0 obj <>
endobj
All rights reserved. By clicking Accept All Cookies, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts. Our habit of giving 360o to a circle, *I am using Babylonian and ancient Mesopotamian interchangeably in this post. mathematical problems and mathematical This page was published over 17 years ago.
The Babylonians had the same system, but they used powers of sixty rather than ten. Knowledge awaits. 0000012830 00000 n
After all, if you were counting things, you would tend to know if you were counting individual things or counting in lots of sixty (or even 3,600!) The Babylonian symbol for one and sixty are the same. Whenever people tell time or make reference to the degrees of a circle, they rely on the base 60 system.